History of Operations Research
The history of operations research (OR) can be traced back to World War II, where mathematicians, statisticians, and other scientists were applying mathematical principles to improve military operations to win the war. Once the war was over, these OR concepts found themselves extremely useful in many parts of civil life and rapidly evolving and developing into many different branches we know today as Mathematical Programming (Linear Programming, Integer Programming, Mixed Integer Linear Programming, Stochastic Integer Programming, Dynamic Programming are typical examples), Artificial Intelligence (Expert Systems, Machine Learning and Deep Learning are great examples) and others. It is, in fact, a near-impossible task to name a sector in modern life that does not use an OR application.
Mathematical Programming
In Mathematical Programming, the methodology is to describe an operation with its properties, actions and operational constraints using mathematical notations so when an objective is given, the performance of that operation can be optimised. This modelling approach can be applied in many areas, from mining operations to logistics, factories, supply chains and so on.
Depending on the nature of objects being described, linear (i.e. continuous) or integer (which includes binary) variables can be used. For example, integral objects like humans, equipment or operational modes can only be denoted using integer variables, while productivity, material flow capacity can be described using linear variables. One important note when formulating mathematical models is that the solution time of solving models increases exponentially according to the number of integer variables to the point that it can be impossible to be solved. On the contrary, pure linear models of any size can be solved in a matter of seconds provided enough computing memory. For this reason, it is critical to keep the number of integer variables as small as possible.
There are some common mathematical models used for optimisation:
- Linear Programming (LP): Contain only linear variables
- Integer Programming (IP): Contain only integer variables
- Mixed Integer Linear Programming (MILP): Contain both linear and integer variables
- Stochastic Integer Programming (SIP): An expansion of MILP that supports modelling uncertainty.
Impacts of Uncertainty on Optimisation
Conventional optimisation models are typically based on an assumption that input data is known with certainty. However, it is fair to say that this critical assumption is hardly true as uncertainty is widely recognised as a nature of almost any dataset. For example, mining projects have seen roughly 30% of failures due to the orebody’s grade and tonnage being overestimated according to several surveys.
An illustration of the two approaches: conventional, deterministic versus risk-based, are presented below. On one hand, a solution is obtained without knowing how close it is to the true but unknown value. On the other hand, the risk-based approach provides both solutions and an associated risk assessment. The philosophy of the new approach can be said as: “It is rather relatively true than precisely wrong”.
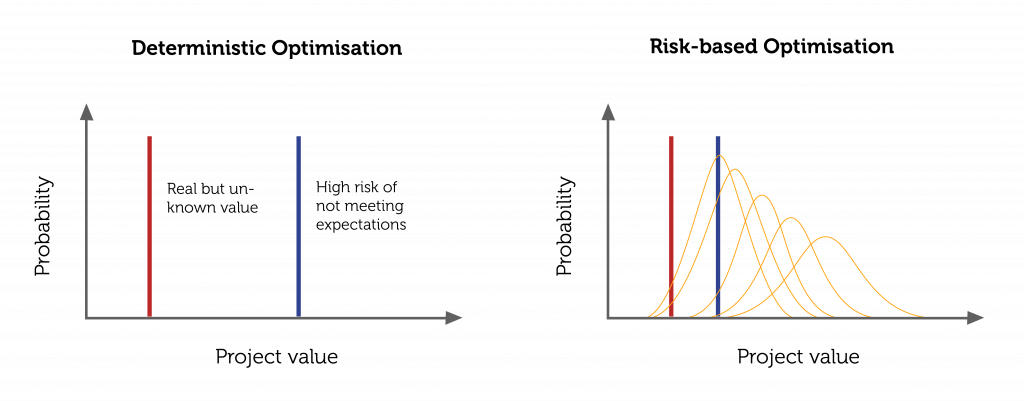

Sources of uncertainty
There are various sources of uncertainty depending on types of projects. One way to categorise is based on whether they can be explicitly modelled and quantified or not.
- Quantifiable uncertainty: Examples in this group are geology, weather, equipment failure, and economic. Geological uncertainty is commonly modelled using geostatistical simulation techniques like Sequential Gaussian Simulation. Other types of uncertainty can be modelled based on historical data using Monte Carlo simulation and its variants.
- Non-Quantifiable uncertainty: Some forms of uncertainty, for example, policy uncertainty, are particularly challenging to model due to implicit factors. The impact of policy uncertainty can be relatively negligible for projects with a lifespan of five years or less but can also be devastating for longer-term ones. For this reason, policy uncertainty is normally treated as scenarios of project perspectives rather than directly embedded into optimisation models.
Risk-based Optimisation Methodology
Initial efforts to incorporate risk into optimisation started in the 1990s where a series of equal possibilities of input data are sequentially fed into an optimisation model and results in a collection of possible outcomes. By analysing this collection using statistical tools like confidence interval analysis, an observation on likely outcomes of the project can be withdrawn. This approach, however, is not able to suggest a unique solution for the problem.
An advancement in this area was made during the 2000s when the above collection of outcomes is post-processed to extract a single solution. During this phase, common features of solutions are honoured, and conflicting ones are merged and mitigated using heuristic rules. Although a single solution can be obtained, there is no guarantee of optimality.
The state-of-the-art methodology to tackle the risk-based optimisation challenge is to use stochastic integer programming (SIP). A SIP model is normally constructed in a way that all possible scenarios of input data are considered simultaneously within the optimisation process. The objective function consists of at least two terms: Term 1: minimise/maximise the key metric of interest such as throughput, cost or profit; Term 2: minimise the risk of not meeting production targets due to the uncertainty of input data. For example in mining projects, the two terms would normally be maximising Net Present Value (NPV) and minimising the risk of not meeting ore quality and tonnage targets.
One recent study (Mai, Topal, Erten, & Sommerville, 2019) detailing the application of SIP on iron ore long-term planning showed that risk-based solution can achieve as much as 7% higher NPV over deterministic solution.
Conclusion
A consensus in the world of risk management is “high-risk high return, low-risk low return”. In the world of stochastic optimisation, however, it is totally possible to have “low-risk high return”. When an operation has a risk-based optimal solution, what else could be better?
About the author
Luan Mai is a Visagio consultant specialised in projects in Optimisation, Simulation, and Data Science with extensive experience in the mining industry. His most current projects are with tier 1 mining companies to deliver optimisation solutions for their supply chain network. He has published 7 papers in ISI journals to detail his research on the application of operations research and machine learning on mineral industries. He holds a PhD in Mine Planning Optimisation from Western Australian School of Mines, Curtin University (Australia).
Reference
Mai, N. L., Topal, E., Erten, O., & Sommerville, B. (2019). A new risk-based optimisation method for the iron ore production scheduling using stochastic integer programming. Resources Policy, 62, 571-579.


